[골드 1] 백준 11401 - 이항 계수 3 (파이썬)
글 작성자: pental

https://www.acmicpc.net/problem/11401
풀이
이게 어떻게 정답률이 40%?
이 문제는 조금 어렵다. 모듈로 연산(1000000007)이 포함된 큰 수의 이항계수를 다루기 때문에, 단순한 팩토리얼 연산으로는 시간 초과가 일어난다.
입력으로는 정수 N, K가 들어오소, 수가 크므로 모듈로 연산이 필요하고, 나눗셈은 페르마의 소정리를 이용해야한다.
먼저 이항 계수 공식은 다음과 같다.
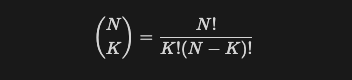
하지만 단순한 팩토리얼 계싼은 값이 너무 커져 오버플로우가 발생하거나 시간초과가 발생한다.
따라서, 문제에서 요구한 1000000007로 모듈로 연산을 적용해야 한다.
왜 일반적인 나눗셈이 안되는 건가요?
→ 일반적으로 모듈러 연산에서는 나눗셈이 직접 불가능하다. → 대신 모둘러 역원을 이용해야한다.
페르마의 소정리는 다음과 같다.
소수 p에 대해서, a^(p - 1) = 1 (mod p)가 성립한다.
즉, 모듈로 소수 p에서 a의 역원은 a^(p - 2) mod 로 계산할 수 있다.
이 문제에서 p = 1000000007로 주어졌으므로 이 정리를 활용할 수 있다.
먼저 팩토리얼 전처리를 진행해야 하며, N!, K!, (N - K)!을 모두 미리 구해서 리스트에 저장한다.
모듈러 역원 계산은 K!과 (N - K)!의 곱의 모듈러 역원을 pow(값, MOD - 2, MOD)로 구한다.
이거 ㄹㅇ 좀 빡쎈문제이다.
코드
# 백준 11401 - 이항 계수 3
# 분류 : 수학
# 문제집 : 단기간 성장 - 4번
MOD = 1_000_000_007
def factorial(N) :
result = [1] * (N + 1)
for i in range(2, N + 1) :
result[i] = result[i - 1] * i % MOD
return result
def mod_inverse(X) :
return pow(X, MOD - 2, MOD)
N, K = map(int, input().split())
fact = factorial(N)
numerator = fact[N]
denominator = fact[K] * fact[N - K] % MOD
result = numerator * mod_inverse(denominator) % MOD
print(result)
'Programming > 백준' 카테고리의 다른 글
| [실버 5] 백준 31738 - 매우 어려운 문제 (파이썬) (0) | 2025.05.03 |
|---|---|
| [골드 4] 백준 10830 - 행렬 제곱 (파이썬) (0) | 2025.05.03 |
| [브론즈 4] 백준 14470 - 전자레인지 (파이썬) (0) | 2025.05.02 |
| [실버 1] 백준 1713 - 후보 추천하기 (파이썬) (0) | 2025.05.01 |
| [브론즈 2] 백준 1173 - 운동 (파이썬) (0) | 2025.05.01 |
댓글
이 글 공유하기
다른 글
-
[실버 5] 백준 31738 - 매우 어려운 문제 (파이썬)
[실버 5] 백준 31738 - 매우 어려운 문제 (파이썬)
2025.05.03 -
[골드 4] 백준 10830 - 행렬 제곱 (파이썬)
[골드 4] 백준 10830 - 행렬 제곱 (파이썬)
2025.05.03 -
[브론즈 4] 백준 14470 - 전자레인지 (파이썬)
[브론즈 4] 백준 14470 - 전자레인지 (파이썬)
2025.05.02 -
[실버 1] 백준 1713 - 후보 추천하기 (파이썬)
[실버 1] 백준 1713 - 후보 추천하기 (파이썬)
2025.05.01